비교해야 할 그룹이 3개 이상이라면 어떻게 해야 할까요? A약, B약, C약의 효과를 한 번에 비교하고 싶을 때 사용하는 것이 바로 ANOVA(Analysis of Variance, 분산분석)입니다.
ANOVA의 핵심 개념인 일원/이원 분산분석과, 모든 통계 분석의 베이스가 되는 정규분포에 대해 정리해 보겠습니다.
1. 분석의 대전제: 정규분포 (Normal Distribution)
ANOVA를 돌리기 전, 우리는 항상 데이터가 정규분포를 따른다는 가정을 확인해야 합니다. 도대체 정규분포가 뭐길래 이렇게 중요할까요?
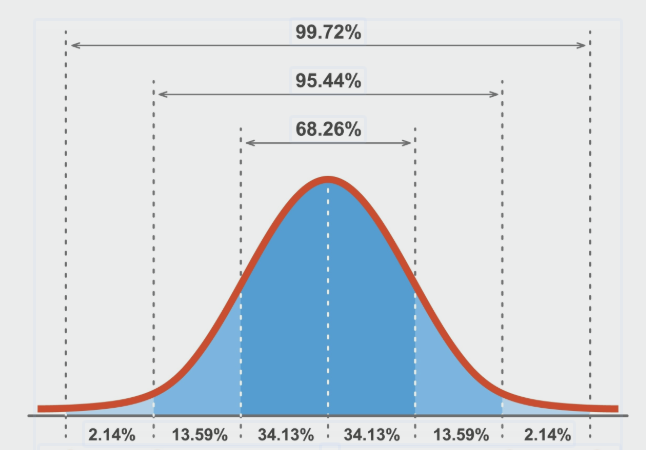
1) 개념: 세상의 질서, 종 모양(Bell Curve)정규분포란 데이터가 평균을 중심으로 좌우 대칭인 종 모양으로 흩어져 있는 분포를 말합니다.
중심: 평균 = 중앙값 = 최빈값. 가장 많은 데이터가 평균 근처에 몰려 있습니다.
양쪽 꼬리: 평균에서 멀어질수록(극단적인 값일수록) 데이터의 개수는 급격히 줄어듭니다.
2) 의료 데이터에서의 의미
"키, 혈압, 혈당 등 자연계의 대부분 생체 신호는 데이터를 많이 모으면 결국 정규분포 모양이 된다"는 믿음(중심극한정리)이 통계의 기초입니다.
표준 정규분포 : 평균이 0, 표준편차가 1인 아주 깔끔한 정규분포.
ANOVA에서의 조건: 엄밀히 말하면 "잔차(Residuals, 모델이 설명 못 하는 오차)"가 정규성을 띠어야 합니다. 실무에서는 각 그룹별 데이터가 정규분포 모양인지 확인합니다. (Shapiro-Wilk 검정 등으로 확인)
2. 왜 T검정을 3번 쓰면 안 될까? (ANOVA의 필요성)
A, B, C 세 그룹이 있을 때, A vs B, B vs C, A vs C 이렇게 T검정을 3번 하면 안 될까요?
문제점: 검정을 반복할수록 1종 오류(Type I Error)가 증가합니다.
비유: 복권(유의수준 5%)을 1장 살 때 당첨 확률과, 3장 살 때 당첨 확률은 다릅니다. T검정을 여러 번 하면 우연히 "차이가 있다"고 잘못 결론 내릴 확률이 급격히 커집니다.
해결책: ANOVA를 사용하여 한 번에 통으로 비교하여 오류를 통제합니다.
3. 일원 분산분석 (One-way ANOVA)
"원인이 딱 1가지"인 경우입니다.
1) 개념 및 가설상황: 하나의 요인에 따라 결과가 달라지는지 봅니다.
의료 예시: 항암제 종류(X)가 A, B, C 3가지일 때, 종양 크기 감소량(Y)의 차이.
귀무가설: 세 그룹의 평균은 모두 같다.
대립가설: 적어도 한 그룹의 평균은 다르다. (어디가 다른지는 안 알려줌 -> 사후검정 필요)
# 방법 1: 간단하게 P-value만 확인 (scipy)
from scipy import stats
# f_oneway: 3개 이상의 그룹 데이터를 입력
f, p = stats.f_oneway(group_A, group_B, group_C)
# 방법 2: 분석가용 테이블 출력 (statsmodels)
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
# C(변수): Categorical(범주형) 변수임을 명시
model = ols('tumor_size ~ C(drug_type)', data=df).fit()
print(anova_lm(model))
# aov: Analysis of Variance
# 종속변수 ~ 독립변수
result <- aov(tumor_size ~ drug_type, data = df)
summary(result)
4. 이원 분산분석 (Two-way ANOVA)
"원인(독립변수)이 2가지"인 경우입니다. 여기서부터 분석의 깊이가 달라집니다.
1) 개념 및 핵심: 교호작용 (Interaction)단순히 요인이 2개인 것뿐만 아니라, 두 요인이 만났을 때 생기는 시너지 효과를 확인합니다.
의료 예시:
요인 1: 운동 유무 (운동 함 / 안 함)
요인 2: 성별 (남 / 여)결과(Y): 체지방 감소량확인해야 할 3가지:운동 효과가 있는가?
(주효과 1)성별에 따라 차이가 있는가?
(주효과 2)"남성이면서 운동을 했을 때" 유독 효과가 큰가?
(교호작용)교호작용이 있다? 그래프를 그렸을 때 선이 평행하지 않고 X자로 교차하거나 기울기가 확연히 다를 때입니다. (예: 운동 효과가 남자한테는 큰데, 여자한테는 별로 없다.)
'Study Note > 통계' 카테고리의 다른 글
| 선형회귀 Part 2: 최소자승법(OLS)과 더미변수 완벽 정리 (0) | 2025.12.12 |
|---|---|
| [머신러닝 기초] 숫자를 예측하는 가장 강력한 직선, 선형회귀(Linear Regression) 완벽 해부 (0) | 2025.12.10 |
| [머신러닝 기초] 통계 예측 모형과 지도학습 (0) | 2025.12.10 |
| 비모수 검정(Non-parametric Test) 총정리 (0) | 2025.12.08 |
| [통계 기초] T검정 vs Z검정, 그리고 양측/단측 검정 정리 (0) | 2025.12.04 |